We investigate the formation of condensates in a binary lattice gas in the presence of chiral interactions. These interactions differ between a given microscopic configuration and its mirror image. We consider a two-dimensional lattice gas with nearest-neighbour interactions, to which we add interactions involving favoured local structures (FLSs) that are chiral. We focus on FLSs that have the shape of the letter L and explore condensate formation through simulations and analytical calculations. At low temperature, this model can exhibit four different phases that are characterised by different periodic tiling patterns, depending on the strength of interactions and the chemical potential. When particle numbers are conserved, some of these phases can coexist. We analyse the structure and surface tension of interfaces between coexisting phases and determine the shapes of minimal free energy of crystalline condensates. We show that these shapes can be quadrilaterals or octagons of different orientation and symmetry.
Publications
Also see Google Scholar or arXiv.
[2024] [2022] [2021] [2020] [2019] [2018] [2017] [2016] [2014] [Viewpoint articles]2024
[20]

[19]
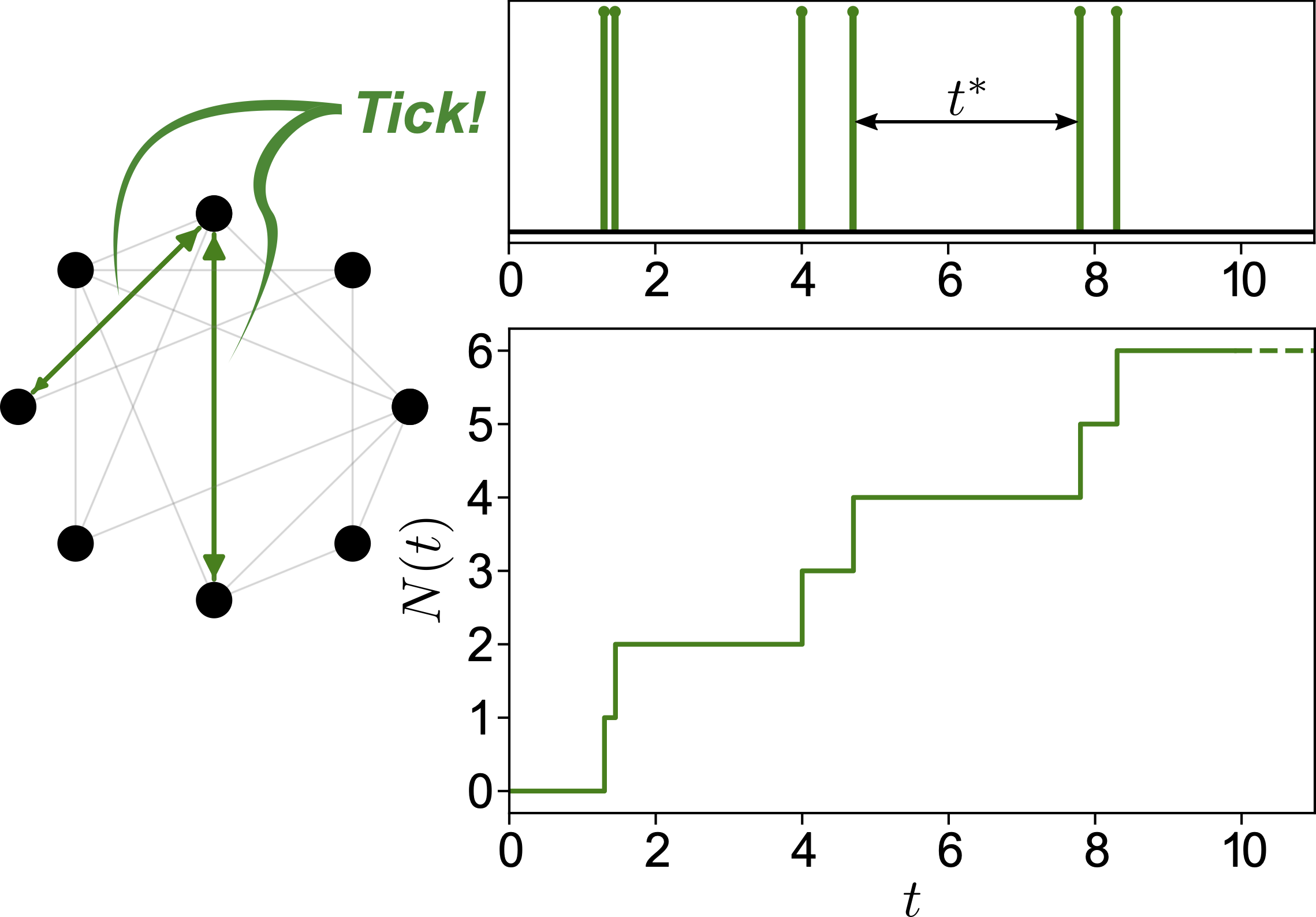
Thermodynamic cost for precision of general counting observables
P. Pietzonka and F. Coghi
Phys. Rev. E 109, 064128 (2024)
Download:
We analytically derive universal bounds that describe the trade-off between thermodynamic cost and precision in a sequence of events related to some internal changes of an otherwise hidden physical system. The precision is quantified by the fluctuations in either the number of events counted over time or the times between successive events. Our results are valid for the same broad class of nonequilibrium driven systems considered by the thermodynamic uncertainty relation, but they extend to both time-symmetric and asymmetric observables. We show how optimal precision saturating the bounds can be achieved. For waiting time fluctuations of asymmetric observables, a phase transition in the optimal configuration arises, where higher precision can be achieved by combining several signals.
2022
[18]
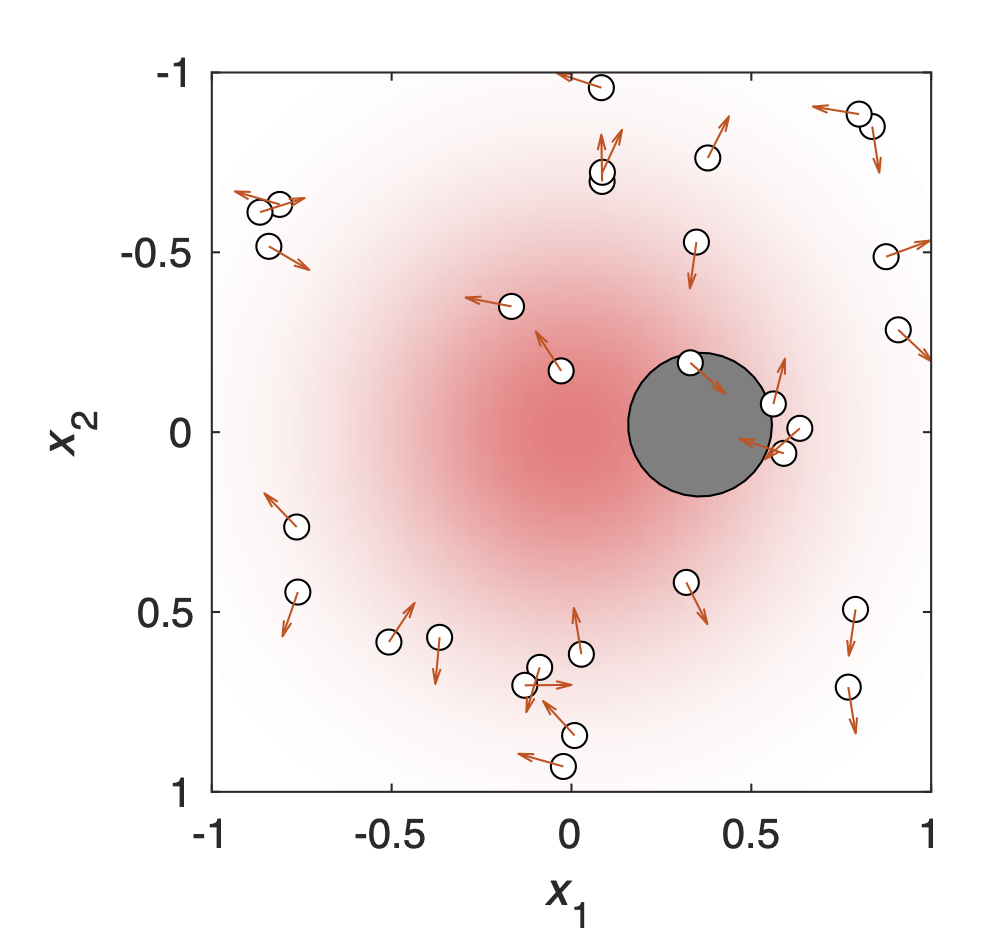
Second Law for Active Heat Engines
A. Datta, P. Pietzonka and A. C. Barato
Phys. Rev. X 12, 031034 (2022)
Download:
Macroscopic cyclic heat engines have been a major motivation for the emergence of thermodynamics. In the last decade, cyclic heat engines that have large fluctuations and operate at finite time were studied within the more modern framework of stochastic thermodynamics. The second law for such heat engines states that the efficiency cannot be larger than the Carnot efficiency. The concept of active cyclic heat engines for a system in the presence of hidden dissipative degrees of freedom, also known as a nonequilibrium or active reservoir, has also been studied in theory and experiment. Such active engines show rather interesting behavior such as an “efficiency” larger than the Carnot bound. They are also likely to play an important role in future developments, given the ubiquitous presence of active media. However, a general second law for cyclic active heat engines has been lacking so far. Here we obtain a general second law for active heat engines, which does not involve the energy dissipation of the hidden degrees of freedom and is expressed in terms of quantities that can be measured directly from the observable degrees of freedom. Besides heat and work, our second law contains an information-theoretic term, which allows an active heat engine to extract work beyond the limits valid for a passive heat engine. Our results come from a known mathematical quantity in stochastic thermodynamics called excess entropy. To obtain a second law expressed in terms of observable variables in the presence of hidden degrees of freedom we introduce a coarse-grained excess entropy and prove a fluctuation theorem for this quantity.
[17]
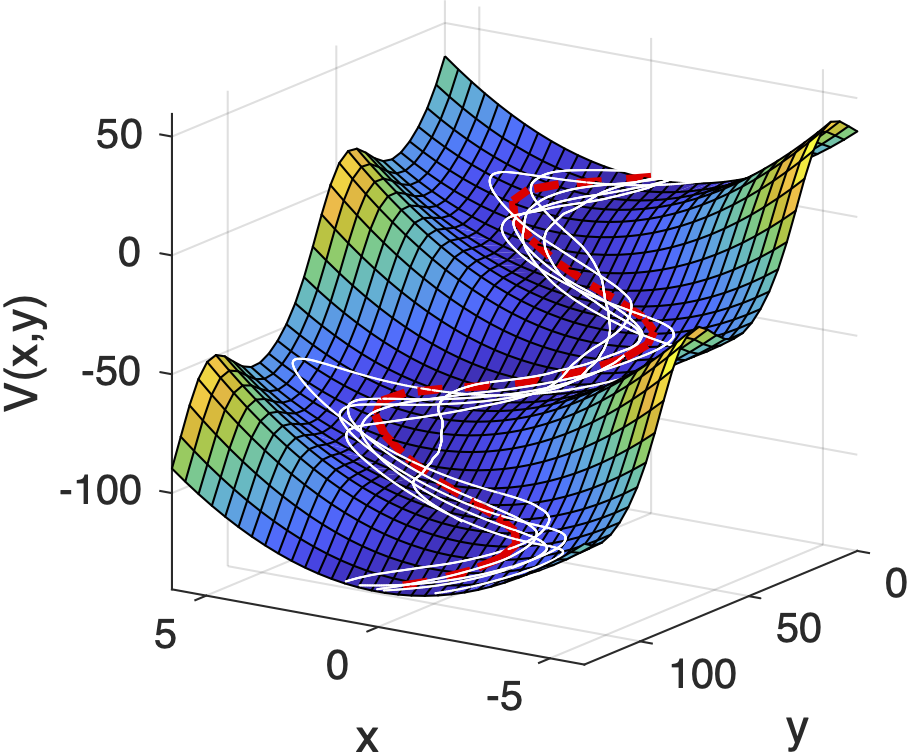
Classical pendulum clocks break the thermodynamic uncertainty relation
P. Pietzonka
Phys. Rev. Lett. 128, 130606 (2022)
Download:
The thermodynamic uncertainty relation expresses a seemingly universal trade-off between the cost for driving an autonomous system and precision in any output observable. It has so far been proven for discrete systems and for overdamped Brownian motion. Its validity for the more general class of underdamped Brownian motion, where inertia is relevant, was conjectured based on numerical evidence. We now disprove this conjecture by constructing a counterexample. Its design is inspired by a classical pendulum clock, which uses an escapement to couple the motion of an oscillator to another degree of freedom (a “hand”) driven by an external force. Considering a thermodynamically consistent, discrete model for an escapement mechanism, we first show that the oscillations of an underdamped harmonic oscillator in thermal equilibrium are sufficient to break the thermodynamic uncertainty relation. We then show that this is also the case in simulations of a fully continuous underdamped system with a potential landscape that mimics an escaped pendulum.
2021
[16]
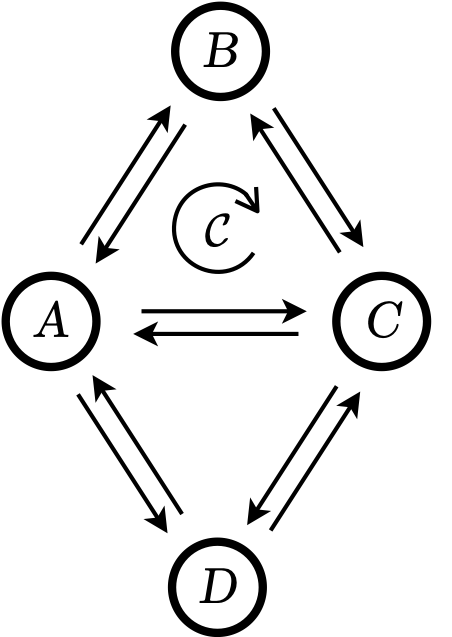
Cycle counts and affinities in stochastic models of nonequilibrium systems
P. Pietzonka, J. Guioth and R. L. Jack
Phys. Rev. E 104, 064137 (2021)
Download:
For nonequilibrium systems described by finite Markov processes, we consider the number of times that a system traverses a cyclic sequence of states (a cycle). The joint distribution of the number of forward and backward instances of any given cycle is described by universal formulas which depend on the cycle affinity, but are otherwise independent of system details. We discuss the similarities and differences of this result to fluctuation theorems, and generalize the result to families of cycles, relevant under coarse graining. Finally, we describe the application of large deviation theory to this cycle-counting problem.
[15]
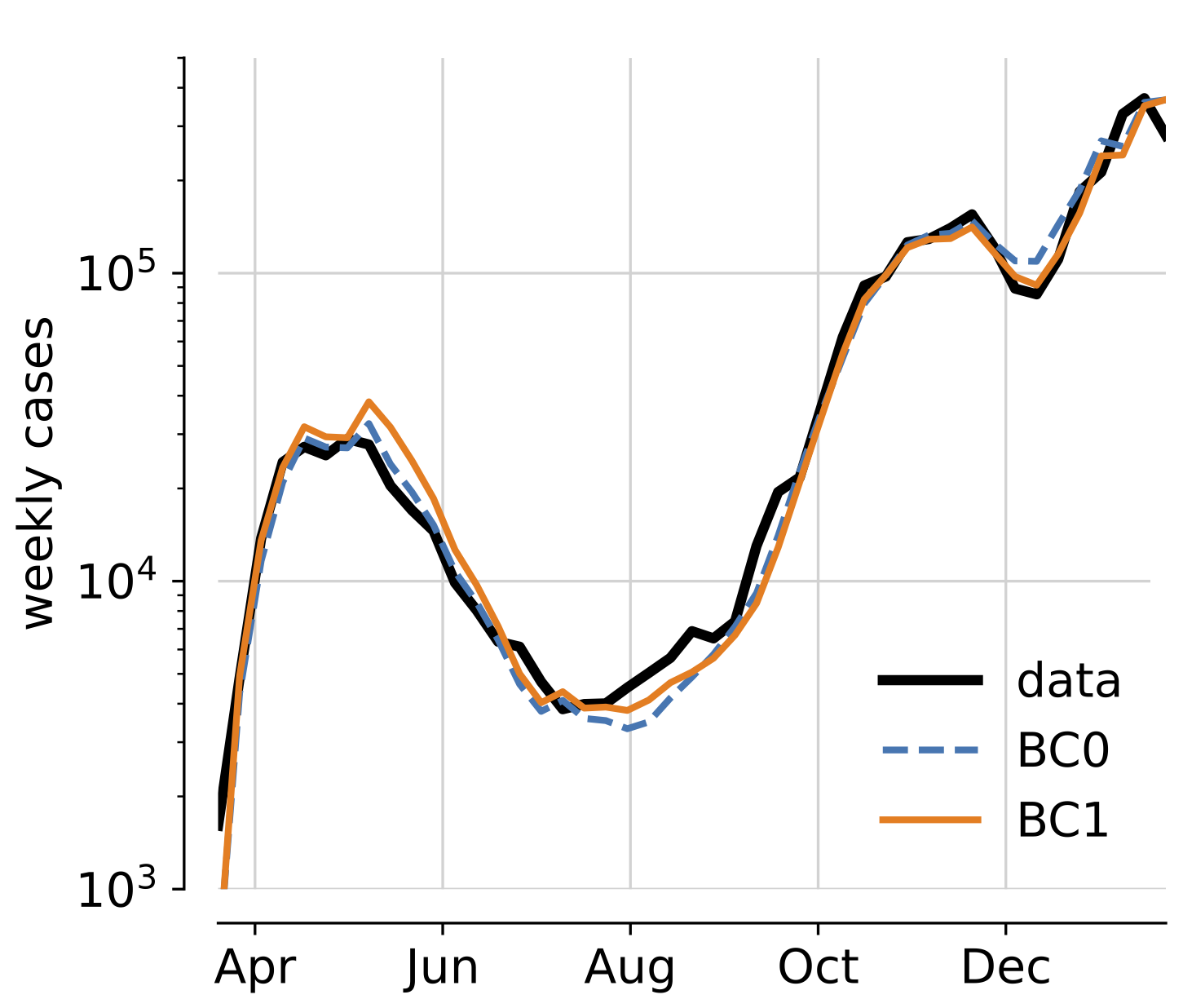
Bayesian inference across multiple models suggests a strong increase in lethality of COVID-19 in late 2020 in the UK
P. Pietzonka, E. Brorson, W. Bankes, M. E. Cates, R. L. Jack and R. Adhikari
PLOS ONE 16, e0258968 (2021)
Download:
We apply Bayesian inference methods to a suite of distinct compartmental models of generalised SEIR type, in which diagnosis and quarantine are included via extra compartments. We investigate the evidence for a change in lethality of COVID-19 in late autumn 2020 in the UK, using age-structured, weekly national aggregate data for cases and mortalities. Models that allow a (step-like or graded) change in infection fatality rate (IFR) have consistently higher model evidence than those without. Moreover, they all infer a close to two-fold increase in IFR. This value lies well above most previously available estimates. However, the same models consistently infer that, most probably, the increase in IFR preceded the time window during which variant B.1.1.7 (alpha) became the dominant strain in the UK. Therefore, according to our models, the caseload and mortality data do not offer unequivocal evidence for higher lethality of a new variant. We compare these results for the UK with similar models for Germany and France, which also show increases in inferred IFR during the same period, despite the even later arrival of new variants in those countries. We argue that while the new variant(s) may be one contributing cause of a large increase in IFR in the UK in autumn 2020, other factors, such as seasonality, or pressure on health services, are likely to also have contributed.
[14]
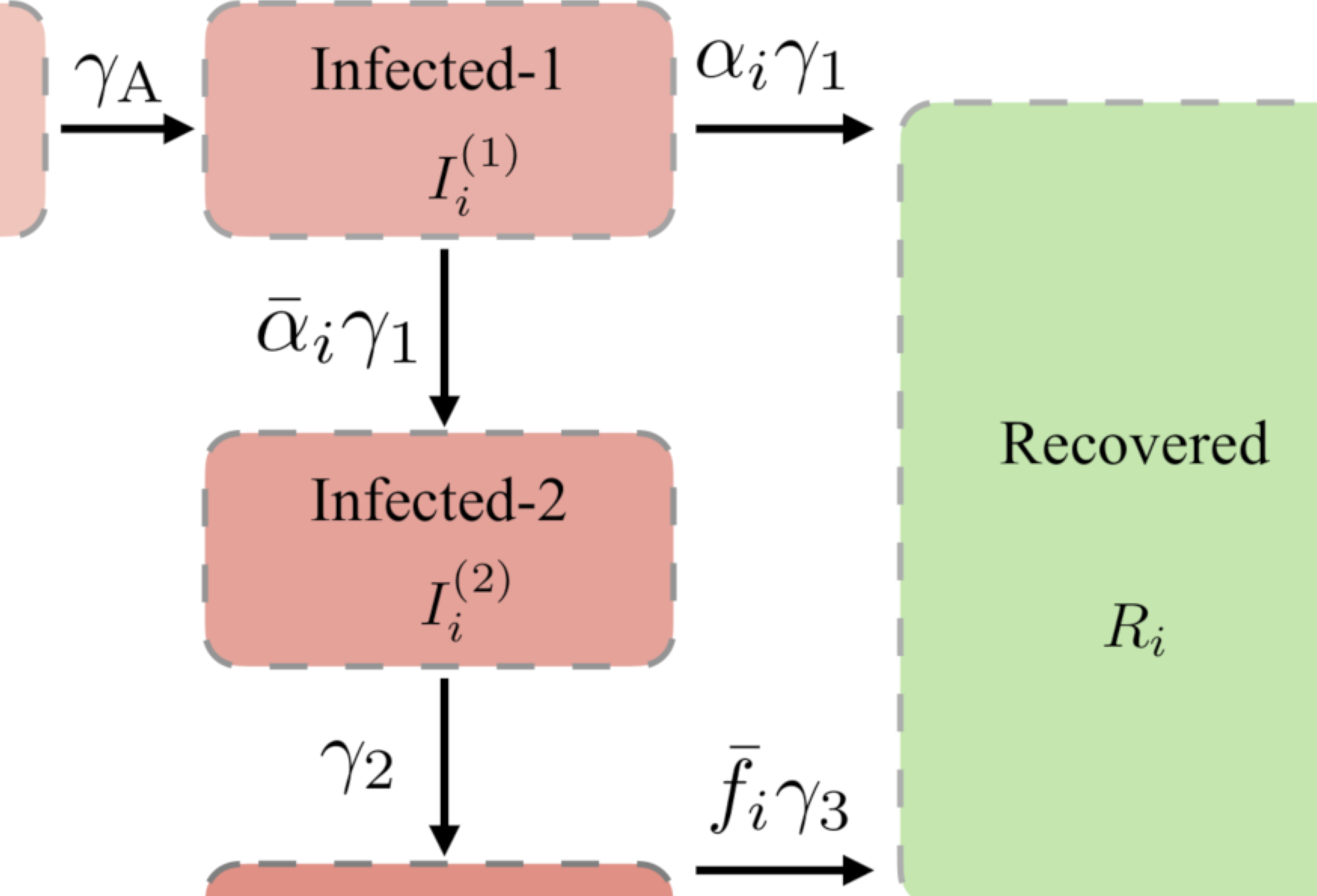
Efficient Bayesian inference of fully stochastic epidemiological models with applications to COVID-19
Y. I. Li, G. Turk, P. B. Rohrbach, P. Pietzonka, J. Kappler, R. Singh, J. Dolezal, T. Ekeh, L. Kikuchi, J. D. Peterson, A. Bolitho, H. Kobayashi, M. E. Cates, R. Adhikari and R. L. Jack
R. Soc. Open Sci. 8, 211065 (2021)
Download:
Epidemiological forecasts are beset by uncertainties about the underlying epidemiological processes, and the surveillance process through which data are acquired. We present a Bayesian inference methodology that quantifies these uncertainties, for epidemics that are modelled by (possibly) non-stationary, continuous-time, Markov population processes. The efficiency of the method derives from a functional central limit theorem approximation of the likelihood, valid for large populations. We demonstrate the methodology by analysing the early stages of the COVID-19 pandemic in the UK, based on age-structured data for the number of deaths. This includes maximum a posteriori estimates, Markov chain Monte Carlo sampling of the posterior, computation of the model evidence, and the determination of parameter sensitivities via the Fisher information matrix. Our methodology is implemented in PyRoss, an open-source platform for analysis of epidemiological compartment models.
2020
[13]
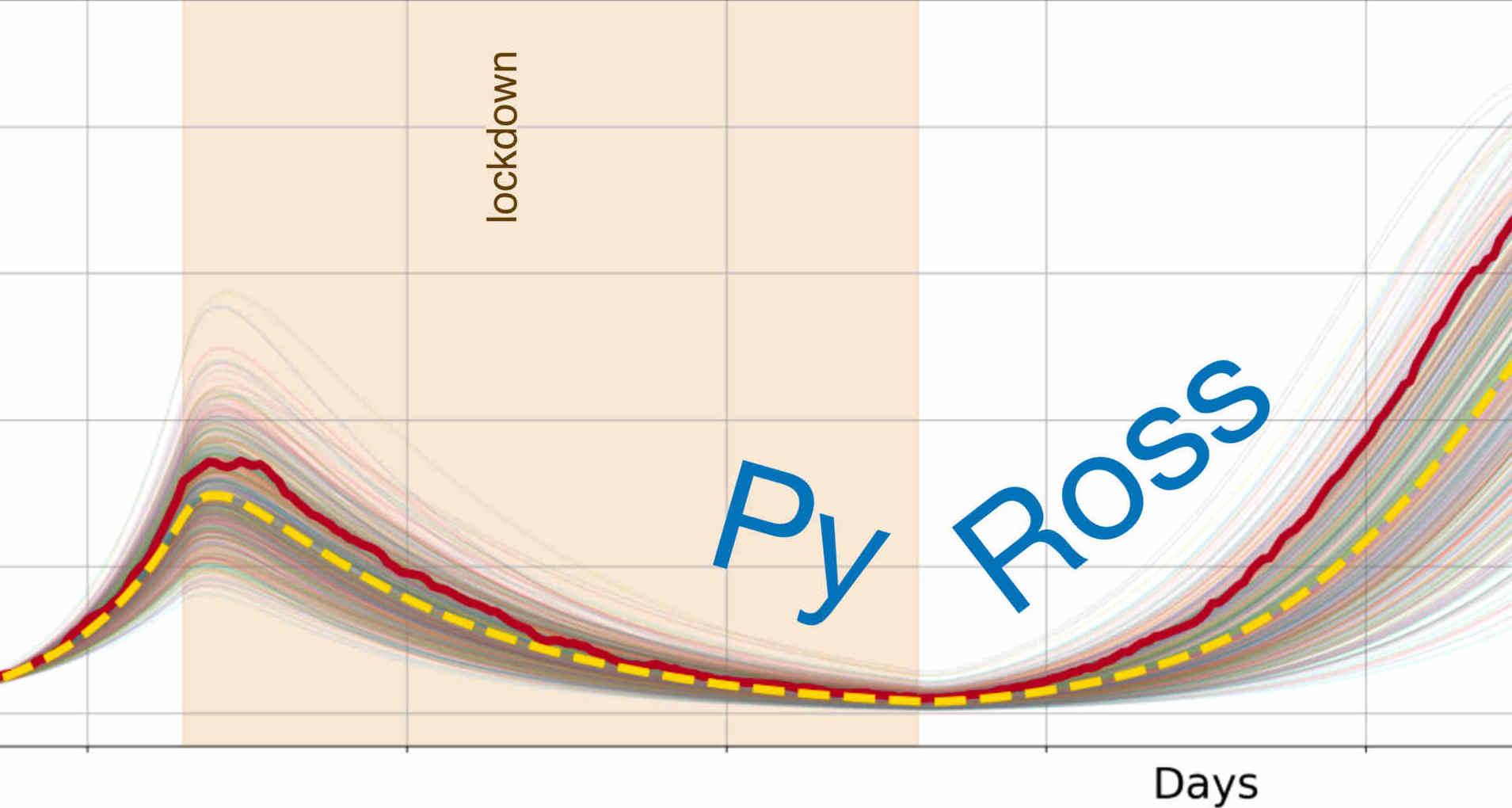
Inference, prediction and optimization of non-pharmaceutical interventions using compartment models: the PyRoss library
R. Adhikari, A. Bolitho, F. Caballero, M. E. Cates, J. Dolezal, T. Ekeh, J. Guioth, R. L. Jack, J. Kappler, L. Kikuchi, H. Kobayashi, Y. I. Li, J. D. Peterson, P. Pietzonka, B. Remez, P. B. Rohrbach, R. Singh and G. Turk
arXiv:2005.09625 Technical Report
Download:
PyRoss is an open-source Python library that offers an integrated platform for inference, prediction and optimisation of NPIs in age- and contact-structured epidemiological compartment models. This report outlines the rationale and functionality of the PyRoss library, with various illustrations and examples focusing on well-mixed, age-structured populations. The PyRoss library supports arbitrary structured models formulated stochastically (as master equations) or deterministically (as ODEs) and allows mid-run transitioning from one to the other. By supporting additional compartmental subdivision ad libitum, PyRoss can emulate time-since-infection models and allows medical stages such as hospitalization or quarantine to be modelled and forecast. The PyRoss library enables fitting to epidemiological data, as available, using Bayesian parameter inference, so that competing models can be weighed by their evidence. PyRoss allows fully Bayesian forecasts of the impact of idealized NPIs by convolving uncertainties arising from epidemiological data, model choice, parameters, and intrinsic stochasticity. Algorithms to optimize time-dependent NPI scenarios against user-defined cost functions are included. PyRoss's current age-structured compartment framework for well-mixed populations will in future reports be extended to include compartments structured by location, occupation, use of travel networks and other attributes relevant to assessing disease spread and the impact of NPIs. We argue that such compartment models, by allowing social data of arbitrary granularity to be combined with Bayesian parameter estimation for poorly-known disease variables, could enable more powerful and robust prediction than other approaches to detailed epidemic modelling. We invite others to use the PyRoss library for research to address today's COVID-19 crisis, and to plan for future pandemics.
2019
[12]
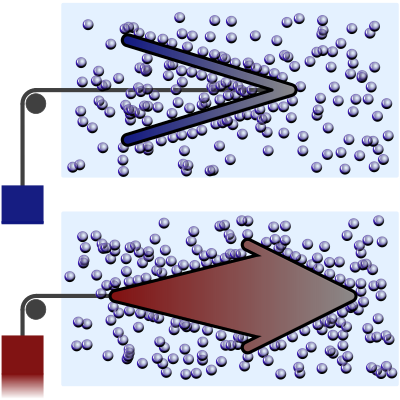
Autonomous engines driven by active matter: Energetics and design principles
P. Pietzonka, É. Fodor, C. Lohrmann, M. E. Cates and U. Seifert
Phys. Rev. X 9, 041032 (2019)
Download:
Because of its nonequilibrium character, active matter in a steady state can drive engines that autonomously deliver work against a constant mechanical force or torque. As a generic model for such an engine, we consider systems that contain one or several active components and a single passive one that is asymmetric in its geometrical shape or its interactions. Generally, one expects that such an asymmetry leads to a persistent, directed current in the passive component, which can be used for the extraction of work. We validate this expectation for a minimal model consisting of an active and a passive particle on a one-dimensional lattice. It leads us to identify thermodynamically consistent measures for the efficiency of the conversion of isotropic activity to directed work. For systems with continuous degrees of freedom, work cannot be extracted using a one-dimensional geometry under quite general conditions. In contrast, we put forward two-dimensional shapes of a movable passive obstacle that are best suited for the extraction of work, which we compare with analytical results for an idealized work-extraction mechanism. For a setting with many noninteracting active particles, we use a mean-field approach to calculate the power and the efficiency, which we validate by simulations. Surprisingly, this approach reveals that the interaction with the passive obstacle can mediate cooperativity between otherwise noninteracting active particles, which enhances the extracted power per active particle significantly.
[11]
A generalization of the thermodynamic uncertainty relation to periodically driven systems
T. Koyuk, U. Seifert and P. Pietzonka
J. Phys. A: Math. Theor. 52, 02LT02 (2019)
Download:
The thermodynamic uncertainty relation expresses a universal trade-off between precision and entropy production, which applies in its original formulation to current observables in steady-state systems. We generalize this relation to periodically time-dependent systems and, relatedly, to a larger class of inherently time-dependent current observables. In the context of heat engines or molecular machines, our generalization applies not only to the work performed by constant driving forces, but also to the work performed while changing energy levels. The entropic term entering the generalized uncertainty relation is the sum of local rates of entropy production, which are modified by a factor that refers to an effective time-independent probability distribution. The conventional form of the thermodynamic uncertainty relation is recovered for a time-independently driven steady state and, additionally, in the limit of fast driving. We illustrate our results for a simple model of a heat engine with two energy levels.
2018
[10]
Universal trade-off between power, efficiency, and constancy in steady-state heat engines
P. Pietzonka and U. Seifert
Phys. Rev. Lett. 120, 190602 (2018)
Download:
Heat engines should ideally have large power output, operate close to Carnot efficiency and show constancy, i.e., exhibit only small fluctuations in this output. For steady-state heat engines, driven by a constant temperature difference between the two heat baths, we prove that out of these three requirements only two are compatible. Constancy enters quantitatively the conventional trade-off between power and efficiency. Thus, we rationalize and unify recent suggestions for overcoming this simple trade-off. Our universal bound is illustrated for a paradigmatic model of a quantum dot solar cell and for a Brownian gyrator delivering mechanical work against an external force.
[9]
Large deviation function for a driven underdamped particle in a periodic potential
L. P. Fischer, P. Pietzonka and U. Seifert
Phys. Rev. E 97, 022143 (2018)
Download:
Employing large deviation theory, we explore current fluctuations of underdamped Brownian motion for the paradigmatic example of a single particle in a one-dimensional periodic potential. Two different approaches to the large deviation function of the particle current are presented. First, we derive an explicit expression for the large deviation functional of the empirical phase space density, which replaces the level 2.5 functional used for overdamped dynamics. Using this approach, we obtain several bounds on the large deviation function of the particle current. We compare these to bounds for overdamped dynamics that have recently been derived, motivated by the thermodynamic uncertainty relation. Second, we provide a method to calculate the large deviation function via the cumulant generating function. We use this method to assess the tightness of the bounds in a numerical case study for a cosine potential.
[8]
Fluctuations of apparent entropy production in networks with hidden slow degrees of freedom
M. Uhl, P. Pietzonka and U. Seifert
J. Stat. Mech.: Theory Exp. 023203 (2018)
Download:
The fluctuation theorem for entropy production is a remarkable symmetry of the distribution of produced entropy that holds universally in non-equilibrium steady states with Markovian dynamics. However, in systems with slow degrees of freedom that are hidden from the observer, it is not possible to infer the amount of produced entropy exactly. Previous work suggested that a relation similar to the fluctuation theorem may hold at least approximately for such systems if one considers an apparent entropy production. By extending the notion of apparent entropy production to discrete bipartite systems, we investigate which criteria have to be met for such a modified fluctuation theorem to hold in the large deviation limit. We use asymptotic approximations of the large deviation function to show that the probabilities of extreme events of apparent entropy production always obey a modified fluctuation theorem and, moreover, that it is possible to infer otherwise hidden properties. For the paradigmatic case of two coupled colloidal particles on rings the rate function of the apparent entropy production is calculated to illustrate this asymptotic behavior and to show that the modified fluctuation theorem observed experimentally for short observation times does not persist in the long time limit.
[7]
Entropy production of active particles and for particles in active baths
P. Pietzonka and U. Seifert
J. Phys. A: Math. Theor. 51, 01LT01 (2018)
Download:
Entropy production of an active particle in an external potential is identified through a thermodynamically consistent minimal lattice model that includes the chemical reaction providing the propulsion and ordinary translational noise. In the continuum limit, a unique expression follows, comprising a direct contribution from the active process and an indirect contribution from ordinary diffusive motion. From the corresponding Langevin equation, this physical entropy production cannot be inferred through the conventional, yet here ambiguous, comparison of forward and time-reversed trajectories. Generalizations to several interacting active particles and passive particles in a bath of active ones are presented explicitly, further ones are briefly indicated.
2017
[6]
Finite-time generalization of the thermodynamic uncertainty relation
P. Pietzonka, F. Ritort and U. Seifert
Phys. Rev. E 96, 012101 (2017)
Download:
For fluctuating currents in nonequilibrium steady states, the recently discovered thermodynamic uncertainty relation expresses a fundamental relation between their variance and the overall entropic cost associated with the driving. We show that this relation holds not only for the long-time limit of fluctuations, as described by large deviation theory, but also for fluctuations on arbitrary finite time scales. This generalization facilitates applying the thermodynamic uncertainty relation to single molecule experiments, for which infinite time scales are not accessible. Importantly, often this finite-time variant of the relation allows inferring a bound on the entropy production that is even stronger than the one obtained from the long-time limit. We illustrate the relation for the fluctuating work that is performed by a stochastically switching laser tweezer on a trapped colloidal particle.
2016
[5]
Universal bound on the efficiency of molecular motors
P. Pietzonka, A. C. Barato and U. Seifert
J. Stat. Mech.: Theor. Exp. 124004 (2016)
Download:
The thermodynamic uncertainty relation provides an inequality relating any mean current, the associated dispersion and the entropy production rate for arbitrary non-equilibrium steady states. Applying it here to a general model of a molecular motor running against an external force or torque, we show that the thermodynamic efficiency of such motors is universally bounded by an expression involving only experimentally accessible quantities. For motors pulling cargo through a viscous fluid, a universal bound for the corresponding Stokes efficiency follows as a variant. A similar result holds if mechanical force is used to synthesize molecules of high chemical potential. Crucially, no knowledge of the detailed underlying mechano-chemical mechanism is required for applying these bounds.
[4]
Affinity- and topology-dependent bound on current fluctuations
P. Pietzonka, A. C. Barato and U. Seifert
J. Phys. A: Math. Theor. 49, 34LT01 (2016)
Download:
We provide a proof of a recently conjectured universal bound on current fluctuations in Markovian processes. This bound establishes a link between the fluctuations of an individual observable current, the cycle affinities driving the system into a non-equilibrium steady state, and the topology of the network. The proof is based on a decomposition of the network into independent cycles with both positive affinity and positive stationary cycle current. This formalism allows for a refinement of the bound for systems in equilibrium or with locally vanishing affinities.
[3]
Universal bounds on current fluctuations
P. Pietzonka, A. C. Barato and U. Seifert
Phys. Rev. E 93, 052145 (2016)
Download:
For current fluctuations in nonequilibrium steady states of Markovian processes, we derive four different universal bounds valid beyond the Gaussian regime. Different variants of these bounds apply to either the entropy change or any individual current, e.g., the rate of substrate consumption in a chemical reaction or the electron current in an electronic device. The bounds vary with respect to their degree of universality and tightness. A universal parabolic bound on the generating function of an arbitrary current depends solely on the average entropy production. A second, stronger bound requires knowledge both of the thermodynamic forces that drive the system and of the topology of the network of states. These two bounds are conjectures based on extensive numerics. An exponential bound that depends only on the average entropy production and the average number of transitions per time is rigorously proved. This bound has no obvious relation to the parabolic bound but it is typically tighter further away from equilibrium. An asymptotic bound that depends on the specific transition rates and becomes tight for large fluctuations is also derived. This bound allows for the prediction of the asymptotic growth of the generating function. Even though our results are restricted to networks with a finite number of states, we show that the parabolic bound is also valid for three paradigmatic examples of driven diffusive systems for which the generating function can be calculated using the additivity principle. Our bounds provide a general class of constraints for nonequilibrium systems.
[2]
Extreme fluctuations of active Brownian motion
P. Pietzonka, K. Kleinbeck and U. Seifert
New J. Phys. 18, 052001 (2016)
Download:
In active Brownian motion, an internal propulsion mechanism interacts with translational and rotational thermal noise and other internal fluctuations to produce directed motion. We derive the distribution of its extreme fluctuations and identify its universal properties using large deviation theory. The limits of slow and fast internal dynamics give rise to a kink-like and parabolic behavior of the corresponding rate functions, respectively. For dipolar Janus particles in two- and three-dimensions interacting with a field, we predict a novel symmetry akin to, but different from, the one related to entropy production. Measurements of these extreme fluctuations could thus be used to infer properties of the underlying, often hidden, network of states.
2014
[1]
Fine-structured large deviations and the fluctuation theorem: Molecular motors and beyond
P. Pietzonka, E. Zimmermann and U. Seifert
EPL 107, 20002 (2014)
Download:
By considering subexponential contributions in large deviation theory, we determine the fine structure in the probability distribution of the observable displacement of a bead coupled to a molecular motor. More generally, for any stochastic motion along a periodic substrate, this approach reveals a discrete symmetry of this distribution for which hidden degrees of freedom lead to a periodic modulation of the slope typically associated with the fluctuation theorem. Contrary to previous interpretations of experimental data, the mean force exerted by a molecular motor is unrelated to the long-time asymptotics of this slope and must rather be extracted from its short-time limit.
Viewpoint articles
The oddity of active matter
P. Pietzonka
Nat. Phys. 17, 1193 (2021)
Download:
Active matter can have macroscopic properties that defy the usual laws of hydrodynamics. Now these tell-tale properties have been traced down to the non-equilibrium character and handedness of interactions between individual particles.